 Prev
Prev
Thursday

 Prev
Prev
|
17 September 98
Thursday |
Next

|
|
Once upon a time, there were three Indian braves. They were great
friends, and they had hunted and fished, and done nearly everything
together all their lives, even unto getting married. Now all of
them had beautiful wives, and all their wives were pregnant with
their first children.
The braves, being braves, were very competitive, and they were equally proud. Each thought his squaw the most beautiful, and each thought that his soon-to-be-born son-- they were each sure their first child would be a son-- would be the lustiest, handsomest child ever born in the tribe. And, in anticipation of the births, each of the braves was trying to outdo the others in preparations. One day, one of the braves returned from a hunting expedition with a buffalo hide, which he presented to his squaw. He told her that she should use the hide when her time came to give birth, to honor her and their son. Not to be outdone, the other two braves went hunting. One returned with a fine bear hide, which he presented to his wife with equal ceremony. The third brave was gone for many days, and his wife and the rest of the tribe were beginning to worry when to the astonishment of all he returned bearing a hippopotamus hide. The tribe and the other braves were impressed, and he presented it to his wife in anticipation of the birth of their son. As it happened, all the squaws went into labor on the same day. The squaw whose husband had given her the bear hide gave birth first, delivering a fine son. Next the squaw whose husband had given her the buffalo hide also delivered fine son. And last of all, the squaw who was laboring on the hippopotamus hide delivered not one, but two fine sons. All the braves were ecstatic, but it was the father of the twins who gleefully observed to the others that the squaw of the hippopotamus equaled the sons of the squaws of the other two hides.
And that is my memory of Johnny Carson's interpretation of Pythagoras' Theorem as told on the Tonight Show, many, many moons ago. If you've never heard of Pythagoras or his Theorem, you probably don't think it's funny. I've always thought it funny, but then, I woke up today thinking about Fermat's Last Theorem. Not that I'm a mathematician, or an intellectual, it's just that math and numbers have always fascinated me-- they seem to have a strange effect on my thinking... I get ideas, and a few weeks ago PBS did a show on the fellow who has proved Fermat's Last Theorem. The show was boring-- they didn't even make an attempt at explaining the proof-- but, even so, I got to thinking... Fermat's Last Theorem ties in directly with Pythagoras' Theorem. Pythagoras, a Greek mathematician who died in 497 B.C., figured out that when it comes to right triangles, the square of the hypotenuse (longest side) is equal to the sum of the squares of the other two sides. (Get it?) Here's a picture you may remember from school:
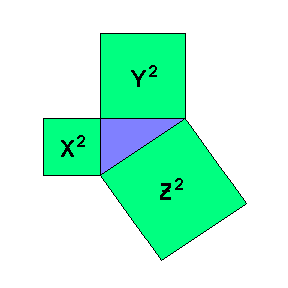
Where X and Y represent the lengths of the perpendicular sides of said right triangle, and Z the hypotenuse of said triangle, it is expressed thus:
a formula students have been plagued with for the last 1700 years-- since Diophantus invented Algebraic notation in the Third Century A.D.-- I bet you had to learn it, too, right? As far as I can recall, it was Euclid (300 B.C.) who delivered up the pre-algebraic Proof that Pythagoras' Theorem worked-- but heck, anybody can prove that one. (If, for instance, X=3, and Y=4, then Z=5 because three squared, or three times itself, equals 9, four squared equals 16, and 9 + 16 = 25, and the square root of 25 is 5. Q.E.D., as they say.) Works great-- and can be demonstrated practically-- artillery men through the ages have been using it to figure out how far away their targets are. But it was Diophantus, 500 years later, who stated the Theorem as the formula X² + Y² = Z², and proved it algebraically. Then he went on to write a book Arithmetica, a definitive treatise on mathematics including all kinds of Theorems and Proofs, which became very popular, and remained in print longer than anything on the N.Y. Times Bestseller List-- long enough in fact, for Pierre de Fermat to pick up a copy in around 1637-- though he may have found it in the leftover bins. Fermat (1601-1665), a Frenchman, was a part-time Parliamentary advisor, and part-time Mathematical hobbyist. Today, he is generally recognized as the inventor of Differential Calculus, but, during his lifetime, almost no one besides his pen pal Mathematician Blaise Pascal knew that the greatest Mathematical Theoretician since Diophantus was doodling in the margins of a copy of Diophantus' Arithmetica, coming up with startling new mathematical Theorems-- and proving them. After Fermat's death, however, his son-- on Pascal's advice probably-- went through the book and decided to publish the margin notes. The most intriguing note was in the margin next to the simple generalization of the XYZ Theorem stated above. It is now known as Fermat's Last Theorem: There do not exist integers [whole numbers] X, Y, and Z, none of which being zero, which satisfy Xn+ Yn = Zn when n is an integer greater than 2. And that Theorem became famous. Why? Because after 1700 years, nobody had ever come up with that particular Theorem, and because in the margin notes next to that startling Theorem, instead of a Proof, this is written: "I have discovered a truly remarkable proof which this margin is too small to contain." If Fermat hadn't already been dead, they'd've had to kill him. Personally, the story makes me wonder. That one Theorem is the only one in the book lacking a marginal Proof (hence "Fermat's Last Theorem"). It has always been acknowledged that the Proof of the Theorem must be a real bear-- it took 300 years for that guy on PBS to come up with his Proof-- so it's understandable that Fermat's "truly remarkable proof" might be too lengthy for inclusion in the margin, but... This is my Theorem: Fermat is one of the great practical jokers of all time. He wrote that tantalizing note for his own amusement, knowing that should any serious Mathematicians like Blaise Pascal ever get a look in his copy of Arithmetica, it would drive them crazy. Of course, I have no Proof.
Like Fermat, I doodle. After drawing the two dimensional version of the formula (squares), I thought I'd try drawing the three dimensional version (cubes), and see if that would shed any light:
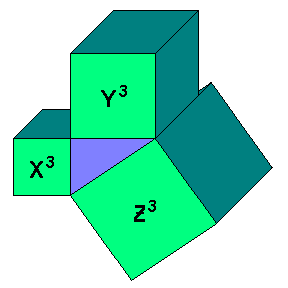
Looking at this drawing it becomes obvoius why Fermat thought he had a provable Theorem... but I got to thinking, what if, instead of substituting numbers for the powers as Mathematicians have always done, we substitute dimensions? In two dimensions-- height and width-- the formula works, as expected, but again, in three dimensions-- height, width, & depth-- it doesn't. But what about the fourth dimension, time? Maybe not, but how many other dimensions are there, anyway? Mightn't there be a dimension out there for which the Xn + Yn = Zn is true? And if there were such a dimension... I find it interesting that two is the only number that "works." One doesn't work. Three or more doesn't work. Only two. Two is a positive integer, a rational number. Only the power of two can solve the equation. Interesting. Interesting, too, that squares are made up of two identical mirrored shapes-- reminds me of a representation of yin and yang... Power of two, yin and yang, male and female... Only the power of two can solve the equation. Is there a human metaphor in there somewhere?
|
|
Please feel free to comment at: The Madwoman's Message Board
|
 Prev
Prev
|
The Madwoman's Journal Index of Entries. |
Next

|